The ACOSH function in Excel is a powerful mathematical tool that calculates the inverse hyperbolic cosine of a number.
While this might sound complex at first, understanding the ACOSH function in Excel can significantly enhance your mathematical calculations and data analysis capabilities.
Whether you’re working with scientific data, engineering calculations, or advanced statistical models, the ACOSH function in Excel provides precise results for hyperbolic calculations.
Many Excel users overlook the ACOSH function in Excel, but it’s an essential tool for anyone dealing with hyperbolic mathematics.
This comprehensive guide will walk you through everything you need to know about using the ACOSH function in Excel effectively, from basic syntax to practical applications.
Table of Contents
🔍 What is the ACOSH Function?
With the ACOSH function, Excel can determine the inverse hyperbolic cosine for a number you provide. In mathematics, if y equals cosh(x), then x can be found using acosh(y).
The function works with values greater than or equal to 1, as the hyperbolic cosine function only produces values in this range.
Understanding the ACOSH function in Excel requires a basic grasp of hyperbolic functions.
These functions are analogous to trigonometric functions but are based on hyperbolas rather than circles.
The hyperbolic cosine function (cosh) and its inverse, the ACOSH function in Excel, are particularly useful in various mathematical and scientific applications.
The mathematical formula for the ACOSH function in Excel is:
ACOSH(x) = ln(x + √(x² - 1))Where x must be greater than or equal to 1.
⚙️ Syntax and Parameters
The syntax for the ACOSH function in Excel is straightforward:
=ACOSH(number)Parameters:
- number: This is the value for which you want to calculate the inverse hyperbolic cosine. You can use this function only when the input is at least 1.
If you provide a value less than 1 to the ACOSH function in Excel, it will return a #NUM! error.
This is because mathematically, the inverse hyperbolic cosine is undefined for values less than 1.

📋 Step-by-Step Guide to Using ACOSH
Basic Usage Example
Let’s begin with a basic example to understand how the ACOSH function works in Excel:
- Open a new Excel worksheet
- Click on cell A1
- Type the formula:
=ACOSH(2)- Press Enter
The result will be approximately 1.316957897, which is the inverse hyperbolic cosine of 2.
Working with Cell References
You can also use the ACOSH function in Excel with cell references:
- Enter the value 3 in cell B1
- In cell B2, enter:
=ACOSH(B1)This approach makes your calculations more dynamic and easier to modify.
📊 Practical Applications and Examples
The ACOSH function in Excel has numerous practical applications across different fields.
Here are some common scenarios where you might use this function:
Engineering Calculations
In engineering, the ACOSH function in Excel is often used for calculating cable tensions, bridge designs, and fluid dynamics problems.
In practical terms, if you need to calculate the form of a suspended cable, also called a catenary curve, Excel’s ACOSH function can help.
Statistical Analysis
Advanced statistical models sometimes require hyperbolic functions.
The ACOSH function in Excel can be particularly useful when working with certain probability distributions or when transforming data for analysis.
Scientific Research
Experts in physics, chemistry, and mathematics often come across problems where the ACOSH function in Excel is needed for accurate calculations.
This includes work with special relativity, quantum mechanics, and thermodynamics.
📈 Common Values and Results Table
Below is a sample table that displays some common inputs along with their outputs using the ACOSH function in Excel:
| Input Value | ACOSH Result | Description |
|---|---|---|
| 1 | 0 | Minimum possible input |
| 1.5 | 0.962424 | Common intermediate value |
| 2 | 1.316958 | Frequently used benchmark |
| 3 | 1.762747 | Standard reference point |
| 5 | 2.292432 | Higher range example |
| 10 | 2.993223 | Large value demonstration |
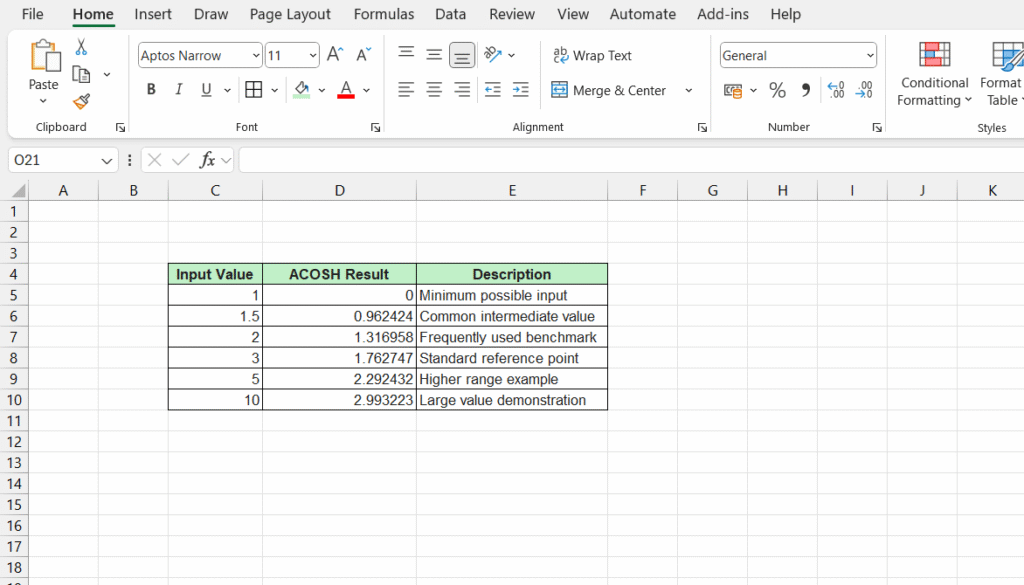
Understanding these common values helps when using the ACOSH function in Excel in real-world scenarios.
Many users find it helpful to reference this table when checking their calculations.
⚠️ Error Handling and Troubleshooting
When working with the ACOSH function in Excel, you might encounter several types of errors:
#NUM! Error
This is the most common error with the ACOSH function in Excel. It occurs when:
- The input value is less than 1
- The input is not a valid number
#VALUE! Error
This error appears when the ACOSH function in Excel receives text or non-numeric data as input.
Solution Strategies
Here are a few guidelines to ensure accuracy when working with the ACOSH function in Excel:
- Always verify that your input values are greater than or equal to 1
- Use data validation to ensure proper input ranges
- Implement error checking with IF statements
Here’s an example of error-safe usage:
=IF(A1>=1, ACOSH(A1), "Invalid input: must be ≥1")🔗 Related Functions and Comparisons
The ACOSH function works alongside other hyperbolic functions in Excel’s mathematical library.
Understanding these relationships can help you use the ACOSH function more effectively.
COSH Function
The COSH function is the inverse of ACOSH. Where ACOSH in Excel determines the inverse hyperbolic cosine, COSH instantly gives the hyperbolic cosine value.
ASINH and ATANH Functions
These are the inverse hyperbolic sine and tangent functions respectively.
Just like the ACOSH function, these are also included in Excel’s wide range of hyperbolic functions.
For a detailed comparison between similar functions, you might want to explore how the ACOS function differs from ACOSH in their applications and mathematical foundations.
💡 Advanced Tips and Techniques
Combining ACOSH with Other Functions
The ACOSH function becomes even more powerful when combined with other Excel functions. Here are some advanced techniques:
Array Formulas
You can use the ACOSH function in Excel with array formulas to process multiple values simultaneously:
=ACOSH(A1:A10)Nested Functions
You can also combine the ACOSH function in Excel with other mathematical functions for more advanced calculations:
=ACOSH(SQRT(B1^2 + 1))Data Analysis Applications
When performing data analysis, the ACOSH function can be part of more complex formulas.
For example, in statistical transformations or when working with exponential growth models.
For advanced problem-solving, analysts commonly embed the ACOSH function into custom macros and formulas in Excel.
This approach streamlines repetitive mathematical operations and ensures consistency across large datasets.
🌟 Best Practices for Using ACOSH
For maximum efficiency while using the ACOSH function, follow these tips:
Input Validation
Always validate your inputs before applying the ACOSH function.
Create robust spreadsheets by implementing proper error checking and data validation rules.
Documentation
When using the ACOSH function in complex formulas, document your calculations clearly.
Future users (including yourself) will appreciate clear explanations of why and how you’re using this function.
Performance Considerations
While the ACOSH function is computationally efficient, be mindful when using it in large datasets or complex array formulas.
Consider breaking down calculations into smaller steps if performance becomes an issue.
🎯 Real-World Examples and Case Studies
Financial Modeling
In advanced financial modeling, the ACOSH function might be used in option pricing models or when working with certain types of volatility calculations.
While not as common as basic arithmetic functions, it serves specific purposes in quantitative finance.
Scientific Computing
Researchers working with hyperbolic geometries or certain physical phenomena rely on the ACOSH function in Excel for accurate calculations.
This includes work in relativity theory, where hyperbolic functions naturally arise.
Quality Control and Statistics
Some statistical distributions and quality control methods utilize hyperbolic functions.
The ACOSH function in Excel provides the essential math base for carrying out complex analytical tasks.
For comprehensive Excel tutorials and advanced function guides, www.techtellent.com offers extensive resources for both beginners and advanced users.
📚 Learning Resources and Further Reading
To deepen your understanding of the ACOSH function in Excel and related mathematical concepts, consider exploring these authoritative resources:
Microsoft’s official Excel documentation provides comprehensive information about all mathematical functions, including the ACOSH function in Excel.
Their support documentation offers detailed explanations and additional examples.
Textbooks on hyperbolic functions provide the theoretical base that can improve how you use the ACOSH function in Excel in real situations.
Understanding the mathematical foundations makes you more effective at applying these functions in real-world scenarios.
🔧 Troubleshooting Common Issues
Users often face specific challenges when implementing the ACOSH function in Excel. Here are solutions to frequent problems:
Precision Issues
When working with very large or very small numbers close to 1, the ACOSH function in Excel might produce unexpected results due to floating-point precision limitations.
In such cases, consider using alternative calculation methods or rounding strategies.
Integration with Other Software
If you’re importing data from other mathematical software packages, ensure that the input format is compatible with the ACOSH function in Excel.
Sometimes data formatting issues can cause unexpected errors.
Performance Optimization
For large datasets, consider using the ACOSH function in Excel efficiently by minimizing recalculations and using appropriate data structures.
❓ Frequently Asked Questions (FAQ)
Q1: What does ACOSH stand for in Excel?
ACOSH stands for “Arc Hyperbolic Cosine” or “Inverse Hyperbolic Cosine.” The ACOSH function in Excel calculates the inverse of the hyperbolic cosine function, returning the value whose hyperbolic cosine equals the input number.
Q2: What happens if I use ACOSH with a number less than 1?
If you input a value less than 1 into the ACOSH function in Excel, you’ll get a #NUM! error. This is because mathematically, the inverse hyperbolic cosine is only defined for values greater than or equal to 1. Always ensure your input values meet this requirement when using the ACOSH function in Excel.
Q3: Can I use ACOSH with negative numbers?
No, the ACOSH function in Excel cannot process negative numbers. Since the domain of the inverse hyperbolic cosine function starts at 1, any negative input will result in a #NUM! error. If you need to work with negative values, consider using other hyperbolic functions like ASINH.
Q4: How is ACOSH different from ACOS in Excel?
While both are inverse functions, ACOS calculates the inverse cosine (trigonometric), while the ACOSH function in Excel calculates the inverse hyperbolic cosine. ACOS works with values between -1 and 1, whereas the ACOSH function in Excel requires values ≥ 1. The mathematical foundations and applications are completely different.
Q5: What’s the minimum value I can use with ACOSH?
The minimum value you can use with the ACOSH function in Excel is exactly 1. When you input 1, the function returns 0, which makes mathematical sense since cosh(0) = 1.
Q6: Is ACOSH available in all Excel versions?
The ACOSH function in Excel is available in Excel 2000 and later versions, including Excel 365, Excel 2021, Excel 2019, Excel 2016, Excel 2013, and Excel 2010. It’s part of Excel’s standard mathematical function library.
🚀 Conclusion
The ACOSH function in Excel is a specialized but valuable tool for mathematical calculations involving inverse hyperbolic cosines.
While it may not be used as frequently as basic arithmetic functions, understanding how to properly implement the ACOSH function in Excel can significantly enhance your analytical capabilities.
From engineering applications to scientific research, the ACOSH function in Excel provides accurate results for complex mathematical operations.
Following these best practices will help you use the ACOSH function in Excel more effectively as part of your mathematical toolkit.
Remember that mastering the ACOSH function in Excel, like any advanced Excel feature, requires practice and application.
It’s best to learn with easy examples before advancing to more challenging applications.
With time and experience, the ACOSH function in Excel will become a natural part of your Excel proficiency.
Whether you’re a student learning advanced mathematics, a professional engineer, or a data analyst working with complex models, the ACOSH function in Excel offers the precision and reliability needed for serious mathematical work.
Take advantage of this powerful function to elevate your Excel skills and tackle more sophisticated analytical challenges.
